java - 求算法. 在球面上取隨機(jī)N個(gè)均勻的點(diǎn)(或者間距不小于某距離的點(diǎn))
問(wèn)題描述
希望能在球上獲得均勻分布, 或者 每?jī)蓚€(gè)點(diǎn)之間的間距不小于某個(gè)值的N個(gè)點(diǎn)的坐標(biāo).點(diǎn)的數(shù)量不需要太大, 在100到200之間就夠用了.球的中心點(diǎn)就是坐標(biāo)系原點(diǎn).
有看到另外一個(gè)大牛寫(xiě)的.https://www.oschina.net/code/...但是傳入100個(gè)點(diǎn)的時(shí)候, 相鄰很近的點(diǎn)出現(xiàn)幾率非常大. 導(dǎo)致在球面上的點(diǎn)上放東西的時(shí)候, 就疊在一起了.
求教, 有沒(méi)有什么其他算法能實(shí)現(xiàn).
問(wèn)題解答
回答1:球面上要實(shí)現(xiàn)均勻采樣不難,用正態(tài)分布隨機(jī)變量產(chǎn)生三維向量再單位化就可以了。

#include <iostream>#include <fstream>#include <random>using namespace std;int main(){ std::default_random_engine gen; std::normal_distribution<float> distrib(0.f, 1.f); ofstream ofs('sphere.txt'); for (int i = 0; i < 1000; i++) {float x = distrib(gen);float y = distrib(gen);float z = distrib(gen);float r = sqrt(x*x + y*y + z*z);ofs << x / r << ’ ’ << y / r << ’ ’ << z / r << endl; } return 0;}
不過(guò)不知道滿不滿足相鄰點(diǎn)之間的要求。如果要保證相鄰點(diǎn)比較遠(yuǎn),可以借鑒一下jittering或者stratified sampling之類的思路。
Java版
import java.util.Random;import java.io.*;class SphericalSampling{ public static void main(String[] args){Random rnd = new Random();try{ PrintWriter writer = new PrintWriter('sphere.txt', 'UTF-8'); for(int i = 0; i < 1000; i++){double x = rnd.nextGaussian();double y = rnd.nextGaussian();double z = rnd.nextGaussian();double r = Math.sqrt(x*x + y*y + z*z);writer.println(x/r + ' ' + y/r + ' ' + z/r); } }catch (Exception e) { e.printStackTrace(System.out);} }}
另外,保存的sphere.txt可以用CloudCompare打開(kāi)查看點(diǎn)云。
回答2:題主的意思是想讓球面上的點(diǎn)間距盡量大,而均勻隨機(jī)分布無(wú)法保證不出現(xiàn)距離任意小的兩點(diǎn),所以這個(gè)題與球面上的隨機(jī)分布無(wú)關(guān)(標(biāo)題太坑人)。
說(shuō)到球面均勻隨機(jī)分布就啰嗦一句。前面@lianera給出的神奇算法我百思不得其解,為啥用正態(tài)分布?后來(lái)從單位化上窺見(jiàn)了端倪:?jiǎn)挝换鋵?shí)是體分布到球面的投影。因?yàn)檎龖B(tài)分布是球?qū)ΨQ的,因此它投影到球面上就一定是均勻的了。也就是說(shuō),真正重要的是分布的球?qū)ΨQ性,具體形式無(wú)所謂。比如圓內(nèi)的面積均勻分布投影可以得到圓上的均勻分布:

網(wǎng)上一搜才發(fā)現(xiàn),原來(lái)這個(gè)問(wèn)題還是蠻有來(lái)頭的,叫做Tamme’s problem,問(wèn)題的解稱為“spherical codes”。這里有一些計(jì)算好的結(jié)果。同時(shí)也知道,當(dāng)點(diǎn)數(shù)比較多時(shí)尋找和證明最優(yōu)解是很困難的。所以題主找到個(gè)還不錯(cuò)的次優(yōu)解就可以啦。
題主給出的鏈接其實(shí)就是基于一種平均化的碼放策略:把球面用緯線平均分成若干個(gè)圓,每個(gè)圓再做等角劃分,但高緯度的圓上方的點(diǎn)少些,低緯度的多些。
最值問(wèn)題要想求得更好的結(jié)果,可以借助各種優(yōu)化工具包求解球面點(diǎn)最小間距的最大值。目標(biāo)函數(shù)直接寫(xiě)成球面點(diǎn)最小間距的形式會(huì)導(dǎo)致函數(shù)穩(wěn)定性很差,不容易求到最優(yōu)解。這里將目標(biāo)函數(shù)取為所有點(diǎn)間距平方的倒數(shù)和并求最小值:
$$text{minimize:} quad sum_{ilt{}j}frac{1}{d^2(i,j)}$$
這樣既突出了相鄰點(diǎn)間距又保持函數(shù)相對(duì)平滑。
我用的是Mathematica提供的NMinimize函數(shù),點(diǎn)數(shù)比較多時(shí)需要很長(zhǎng)計(jì)算。比如在我機(jī)器上算160個(gè)點(diǎn)需要四個(gè)小時(shí)。結(jié)果畫(huà)圖:
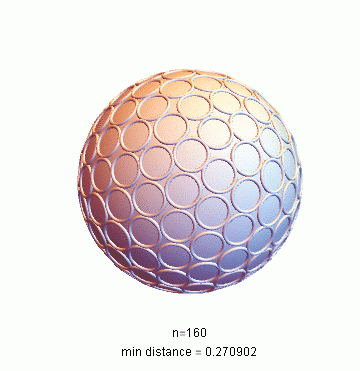
相關(guān)文章:
1. Docker for Mac 創(chuàng)建的dnsmasq容器連不上/不工作的問(wèn)題2. docker - 如何修改運(yùn)行中容器的配置3. docker安裝后出現(xiàn)Cannot connect to the Docker daemon.4. nignx - docker內(nèi)nginx 80端口被占用5. python3.x - python連oanda的模擬交易api獲取json問(wèn)題第五問(wèn)6. javascript - QWebEngineView 如何爬 angular 的動(dòng)態(tài)數(shù)據(jù)?7. css3 - 沒(méi)明白盒子的height隨width的變化這段css是怎樣實(shí)現(xiàn)的?8. javascript - webpack熱加載配置不生效9. java - SSH框架中寫(xiě)分頁(yè)時(shí)service層中不能注入分頁(yè)類10. java - instance method中 static后的<K>是什么意思?
 網(wǎng)公網(wǎng)安備
網(wǎng)公網(wǎng)安備